
Projet : Jeu de dés
Introduction
Le jeu de dés est un jeu à un joueur. Les règles du jeu sont à première vue simple, on a un nombre de départ disons "n" et trois dés, un dé de 4 faces un dé de 6 faces et un de 8. À chaque tour, le joueur doit choisir un dé et on soustrait le nombre du dé au nombre de départ le but étant de finir à 0 ou sinon, c'est perdu.
Ici nous allons donc nous intéressé a trouver le meilleur dé pour avoir le plus de chance de gagner pour un "n" donné.
Il ressemble à première vue beaucoup au jeu de Nim, mais il est radicalement différent. Nous allons donc dans un premier temps évoquer les stratégies de jeu qui nous sont venues à l'esprit puis ensuite essayées de trouver la stratégie la plus optimale. Pour finir, nous allons essayer de généraliser le problème.
À première vue, plusieurs stratégies peuvent nous venir à l'idée, nous allons donc essayer d'en analyser plusieurs et de voir comparées les probabilités de victoire de chacune. (On prend le jeu de dés [4 : 6 : 8] Pour tous les tests)
- La première idée qui nous vient à l'esprit et donc de tester chaque dé un par un :
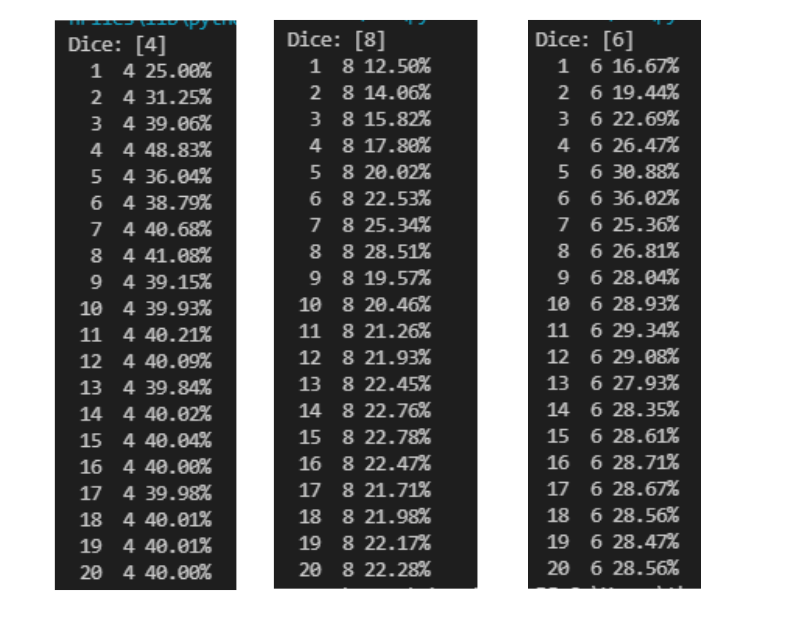
On peut donc déjà conclure une première chose. Plus le dé est grand moins on a de chance de gagner maintenant essayons de voir si en prenant les dés de façon plus "intelligente" on arrive à avoir une meilleure probabilité de victoire.
2. Maintenant, essayons de nous pencher plus sur la question. On s'est donc demandé pourquoi ne pas prendre le dé de 8 tant que n > 8 puis le dé de 6 tant que n > 6 et enfin le dé de 4 :
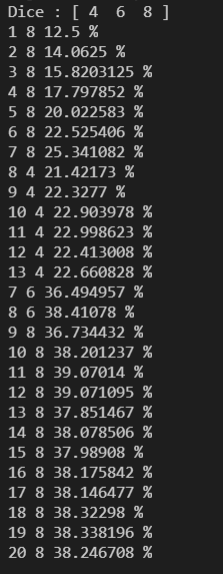
Malheureusement, la probabilité obtenue n'est pas satisfaisante. On se retrouve donc avec une chance de gagner inférieur a celle lorsque l'on joue uniquement le jeu de 4.
3. Enfin, essayons de prendre le plus grand diviseur du nombre et dans le cas où le nombre n'y en à pas prendre le plus petit dé possible ce qui nous donne :
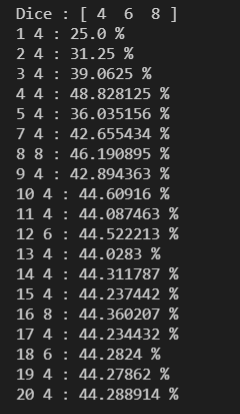
On voit directement que nous obtenons une meilleure probabilité de gagner qu'avec les autres stratégies, maintenant reste à savoir si nous avons trouvé la meilleure probabilité...
Afin de Résoudre ce problème de façon optimal, il nous faut connaître le taux de victoire de chaque dé. En effet la stratégie optimal va consister à choisir le dé qui a le plus de chance de victoire pour un n donné.
On va donc avoir une formule de la forme :
P(n) = Max ( P4 (n); P6 (n) ; P8 (n) )
où Pk (n) est la probabilité de gagner avec le dé à k faces.
Il faut maintenant calculer la chance de victoire pour chaque dé :

Cette formule exprime les chances de gagner avec un dé à k faces à l'indice n.
Il s'agit en fait de la moyenne des probabilités optimales des évènements qu'on peut obtenir avec le dé k . On fait ici une moyenne car tout les évènements on la même chance de se produire, on a une équiprobabilité.
Par exemple les chances de victoires avec le dé 4 quand on est à 10 sont :

On a donc une définition récursive de la probabilité. On connait maintenant le moyen de calculer toutes les chances de victoires pour chaque dé en suivant la la stratégie optimal. On aura donc juste à choisir le dé ayant la probabilité la plus élevée !
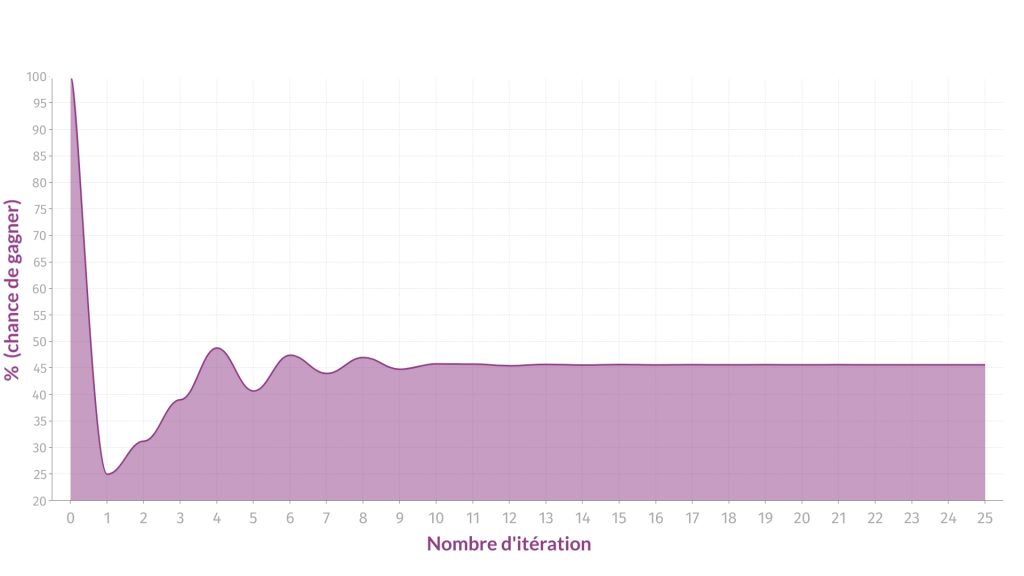
On peut se demander si le résultat obtenu pour la probabilité d'un dé k est bien compris entre zéro et un donc que ce soit bien une probabilité.
Pour ce calcul on calcul une moyenne or par définition une moyenne ne peut pas être plus grande que l'élément maximal et plus petit que l'élément minimal.
Il suffit alors de démontrer qu'on a aucun éléments plus grand que 1 et plus petit que 0.
On sait que le calcul des probabilités se fait de façon récursive, or on sait que pour tout x <1 : P(x) = 0 et P(1) = 1
pour tout n >1 : P(n) est une moyenne des probabilités de P(n-1) à P(n-k) si le dé à k faces est celui donnant les meilleurs chances de réussite.
Or P(n-1) est une moyenne des probabilités de P((n-1)-1) à P((n-1)-j) où j est le dé à j faces donnent les meilleurs chances de réussite.
Il existe n>1 tel que (n-k) < 1
donc on peut écrire P(n) sous la forme de moyennes récursives avec pour éléments initiaux P(1) et P(x) (x <1)
Par récurrence on peut dire que P(n) est une moyenne dont les éléments initiaux sont 0 et 1. Alors P(n) est bien compris entre 0 et 1 d'après la propriété de la moyenne.
P(n) est donc bien une probabilité.
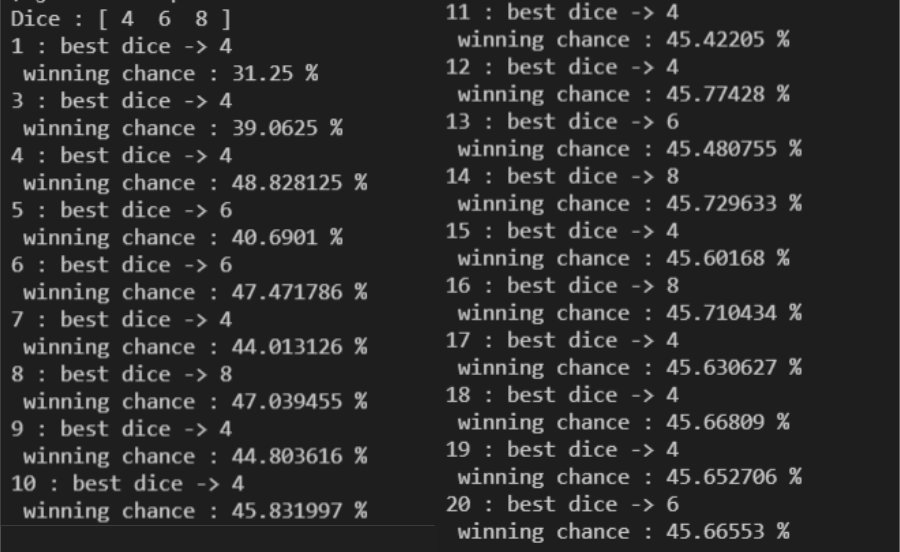
On peut aussi remarquer sur la courbe que la probabilité tend vers une limite fini. Cependant les valeurs oscillent entre cette limite jusqu'à un certain point qui ici semble être 15 dû au erreur d'approximation.
Or il s'avère que cette oscillation est le résultat de la récursion de moyenne. Une moyenne par définition sert à "lisser" des résultats afin de les interpréter.
Notre probabilité qui n'est en faite qu'une récursion de moyenne va donc subir ce lissage progressif et finir par tendre vers une limite qui pour ce problème semble être 45.66%.
Généralisation du problème
On a trouvé une formule récursive qui nous permet de calculer les probabilités de victoire en suivant la stratégie optimale. On cherche maintenant à généralisé le problème avec un nombre k de dés ayant tous un nombre de faces différent.
La stratégie optimale elle ne change pas, il nous suffit toujours de prendre le dé nous offrant le meilleurs taux de victoire à l'indice n donné.
Soit D notre ensemble de dé tous distincts :

Le calcul de probabilité pour chaque dé lui ne change pas il vaut :

où k est le nombre de face du dé d.
On peut employé le même raisonnement que dans le cas particulier, P(n) sera bien une probabilité car il est compris entre 0 et 1 du fait d'être une récursion de moyenne.
De la même façon P(n) va tendre vers une limite à cause du "lissage" des moyennes consécutives.
Bibliographie
Pour ce projet nous avons créés un programme n'ont pas en p5.js mais en java car il ne nécessite pas d'interface graphique. Voici donc le lien GitLab du projet qui fonctionne parfaitement sur n'importe quelle OS tant que Java est installée :
https://gaufre.informatique.univ-paris-diderot.fr/sonnevil/projetmathdiscrete
Les sites sur lesquels nous avons basé notre raisonnement :
– https://blog.plover.com/math/dice-game.html (1)
-https://math.stackexchange.com/questions/4192238/convergence-of-winning-probability-in-a-one-player-dice-throwing-game
